ইয়াং এর পরীক্ষা

ইয়ং এর ব্যতিচারের  ব্যবহৃত আলোর তরঙ্গদৈর্ঘ্য 3890Å,চিড়দ্বয়ের মধ্যবর্তী দূরত্ব 1mm এবং পরপর দুইটি ডোরার দূরত্ব 0.1mm,  পর্দা হতে চিড়ের দূরত্ব কত?

BUET 21-22

Ans:

<span>Δx=λDa⇒D=0.1×10−3×1×10−33890×10−10=0.257 m<span> \Delta \mathrm{x}=\frac{\lambda \mathrm{D}}{\mathrm{a}} \Rightarrow \mathrm{D}=\frac{0.1 \times 10^{-3} \times 1 \times 10^{-3}}{3890 \times 10^{-10}}=0.257 \mathrm{~m}

<span>Δx=λDa⇒D=0.1×10−3×1×10−33890×10−10=0.257 m<span> \Delta \mathrm{x}=\frac{\lambda \mathrm{D}}{\mathrm{a}} \Rightarrow \mathrm{D}=\frac{0.1 \times 10^{-3} \times 1 \times 10^{-3}}{3890 \times 10^{-10}}=0.257 \mathrm{~m}

ইয়াং এর পরীক্ষা টপিকের ওপরে পরীক্ষা দাও

এখনো না বুঝতে পারলে ডাউটস এ পোস্ট করো

পোস্ট করো

Related question

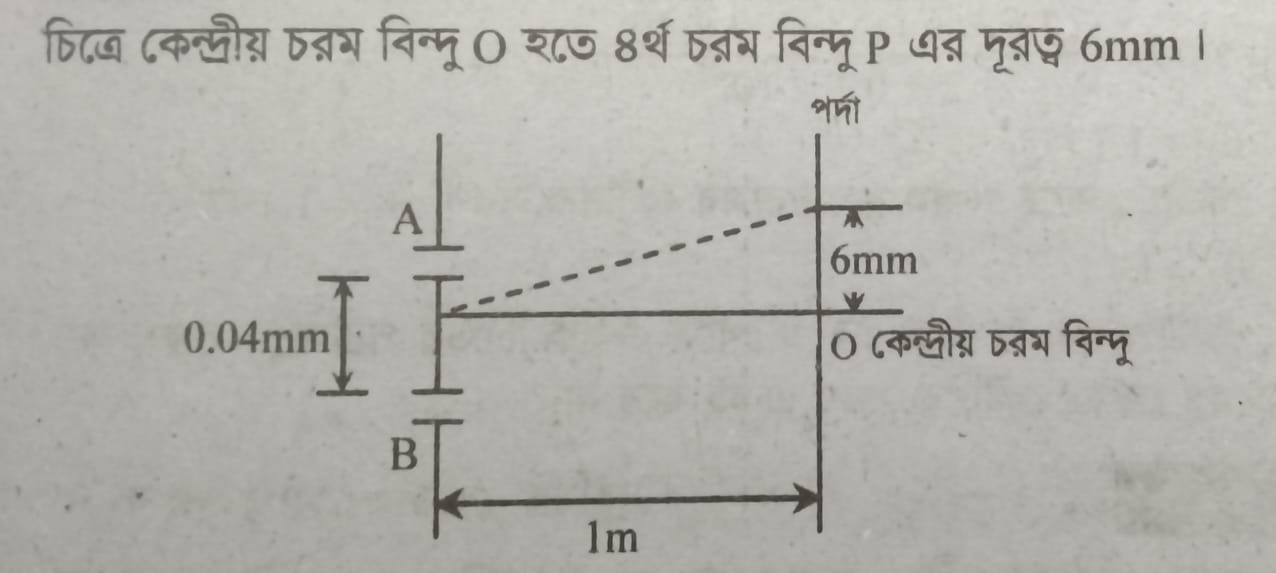
ইয়ং-এর দ্বি চির পরীক্ষায় চির দুটির মধ্যবর্তী দূরত্ব, d = 2 mm। চির থেকে পর্দার দূরত্ব, D = 10⁴ mm। ডোরার প্রস্থ x = 0.3mm।

D-কে যথেচ্ছ বৃদ্ধি করা সম্ভব নয় কারণ - 

ইয়ং-এর দ্বি-চিড় পরীক্ষায় বেগুনি ( λ = 4000 A°) এবং লাল ( λ = 8000 A°) বর্ণের আলোর জন্য ব্যতিচার ঝালর প্রস্থের অনুপাত হলো-

দুটি সরু চিড় পরস্পর হতে 4 mm দূরে অবস্থিত। এ ব্যবস্থাকে 5890 Å তরঙ্গদৈর্ঘ্যের  আলোক দ্বারা আলোকিত করা হলে 0.8 m দূরে অবস্থিত পর্দায় উজ্জ্বল ও অন্ধকার ডোরার সৃষ্টি হলো।

কেন্দ্রীয় চরম থেকে 0.047 cm দূরে কত ক্রমের উজ্জ্বল ডোরা পাওয়া যায়?

চিত্রে ইয়ং এর দ্বি-চিড় পরীক্ষার ব্যবস্থা দেখানো হয়েছে। ব্যবহৃত আলোর তরঙ্গদৈর্ঘ্য 5500Å, চিড়দ্বয়ের প্রস্থ 0.1 mm এবং মধ্যবর্তী দূরত্ব 0.5 mm। পানির প্রতিসরাঙ্ক 1.33 এবং পানিতে আলোর দ্রুতি 1450 ms−1ms^{-1}।