পাহাড়ের উচ্চতা নির্ণয়
একটি সেকেন্ড দোলক ঘড়ি পাহাড়ের পাদদেশে ঠিক সময় দেয় কিন্তু পাহাড়ের চূড়ায় উঠালে 2 ঘন্টায় 8 সেকেন্ড সময়ের পার্থক্য দেখায়। পৃথিবীর ব্যাস 12800 km হলে-
(i) পাহাড়ের উচ্চতা নির্ণয় কর।
(ii) পাহাড়ের চূড়ায় সঠিকভাবে কাজ করতে হলে দোলকের দৈর্ঘ্য কত % পরিবর্তন করতে হবে?
(i) প্রশ্নমতে, পাহাড়ের উপর ঘড়ি 2 ঘন্টায় সেকেন্ড ধীরে চলে।
সুতরাং 24 ঘন্টায় ধীরে চলে সেকেশ্ড।
এখন পাহাড়ের পাদদেশে দোলনকাল এবং পাহাড়ের চূড়ায় দোলনকাল হুলে
পাহাড়ের উচ্চতা , পাদদেকে অভিকর্ষজ ত্বরণ এবং চূড়ায় অভিকর্ষজ ত্বরণ হনে
আমরা জানি,
(ii) পাদদেশে দোলকের টৈর্ঘ্য
পাহাড়ের চূড়ায় করনে দোলনকাল অপরিবর্তিত থাকবে।
আমরা জানি, সুতরাং
সুতরাং [ (i) হতে ]
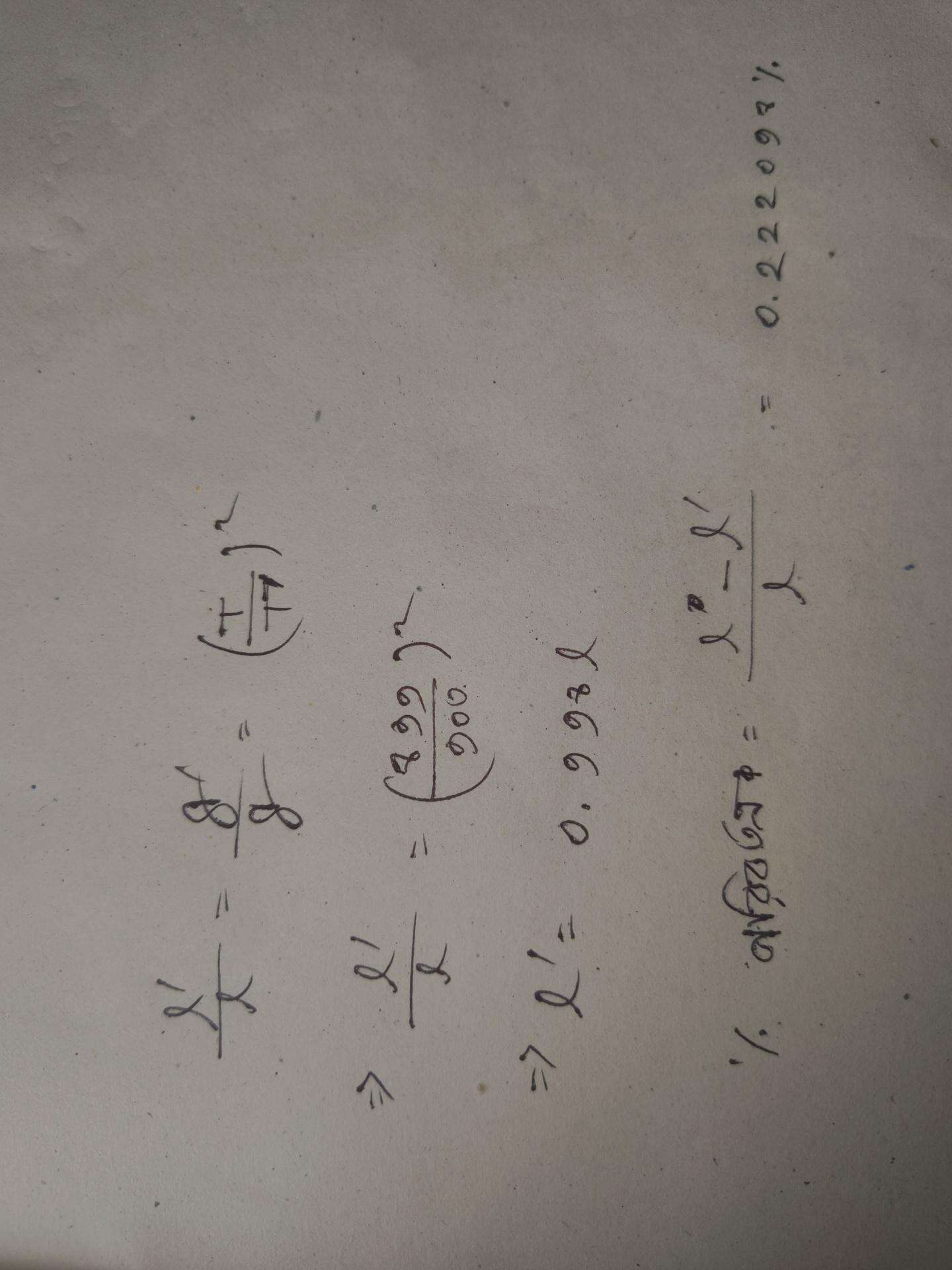
Ai এর মাধ্যমে
১০ লক্ষ+ প্রশ্ন ডাটাবেজ
প্র্যাকটিস এর মাধ্যমে নিজেকে তৈরি করে ফেলো
উত্তর দিবে তোমার বই থেকে ও তোমার মত করে।
সারা দেশের শিক্ষার্থীদের মধ্যে নিজের অবস্থান যাচাই
ভূপৃষ্ট থেকে একটি সেকেন্ড দোলক কত উচ্চতার পাহাড়ে উঠালে সারাদিনে ১ মিনিট ধীরে চলবে?
একটি পেন্ডুলাম ঘড়ি ভূপৃষ্ঠে প্রতি সেকেন্ডে 1টি অর্ধদোলন দেয়। কিন্তু পাহাড়ের উপর নিয়ে গেলে দৈনিক 100 s সময় হারায়। পৃথিবীর ব্যাসার্ধ 6400 km এবং পৃথিবী পৃষ্ঠে অভিকর্ষজ ত্বরণ 9.8 m s–2।
ফাহিম বান্দরবানে বেড়াতে গিয়ে একটি দোলককে পাহাড়ের পাদদেশে নিয়ে গেলে 2 sec এ একটি পূর্ণদোলন সম্পন্ন করে। এরপর সে দোলকটিকে উক্ত পাহাড়ের চূড়ায় নিয়ে গেলে সেটি ঘণ্টায় 30 sec সময় হারায়। পৃথিবীর ব্যাস 12800 km।
একটি সেকেন্ড দোলক ভূ-পৃষ্ঠে সঠিক সময় দেয়। একে পাহাড়ের ওপর নিয়ে গেলে তা প্রতিদিন 10 sec সময় হারায়।
[পৃথিবীর ব্যাসার্ধ, R = 6400 km এবং ভূ-পৃষ্ঠের অভিকর্ষীয় ত্বরণ ]