তড়িত দ্বিমেরু

কোনো তড়িৎ দ্বিমেরুর অক্ষের উপর মধ্যবিন্দু হতে rr দূরত্বে কোনো বিন্দুতে তড়িৎ বিভব হলো—

Din B 22

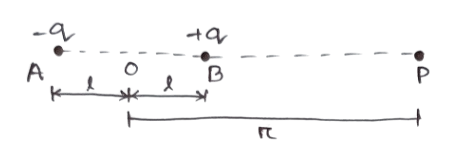A বিন্দুর জন্য P বিন্দুর বিভব

VA=14πε0⋅−q(π+l) V_{A}=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{-q}{(\pi+l)}

B বিন্দুর জন্য P বিন্দুর বিভব

VB=14πε0⋅q(π−l) V_{B}=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{(\pi-l)}

এখন, এ বিন্দুর বিভব V=VA+VB V=V_{A}+V_{B}

=14πε0[−qπ+l+qπ−l]=q4πε0[π+l−π+lr2−l2]∴V=14πε0⋅q⋅2lr2−l2=14πε0⋅pr2−l2[p=q×2l] \begin{aligned} & =\frac{1}{4 \pi \varepsilon_{0}}\left[\frac{-q}{\pi+l}+\frac{q}{\pi-l}\right] \\ & =\frac{q}{4 \pi \varepsilon_{0}}\left[\frac{\pi+l-\pi+l}{r^{2}-l^{2}}\right] \\ \therefore V & =\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q \cdot 2 l}{r^{2}-l^{2}} \\ & =\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{p}{r^{2}-l^{2}}[p=q \times 2 l]\end{aligned}

তড়িত দ্বিমেরু টপিকের ওপরে পরীক্ষা দাও

এখনো না বুঝতে পারলে ডাউটস এ পোস্ট করো

পোস্ট করো

Related question

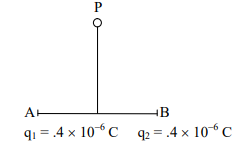
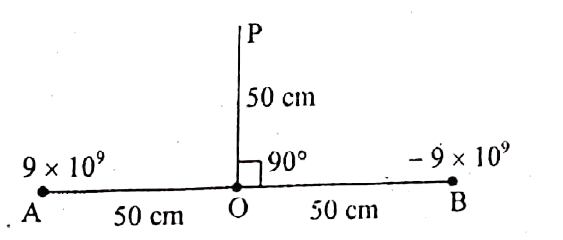
একটি তড়িৎ দ্বিমেরু 1×10−4 1 \times 10^{-4} কুলম্ব মানের দুইটি বিপরীত চার্জ দ্বারা গঠিত এবং তাদের মধ্যবর্তী দূরত্ব 2 সে.মি, দ্বিমেরুটি 1×105NC−1 1 \times 10^{5} \mathrm{NC}^{-1} তড়িৎ ক্ষেত্রে স্থপিত। দ্বিমেরুটিকে ঘুরিয়ে বিপরীত অভিমুখে স্থাপন করতে কী পরিমাণ কাজ করতে হবে?

ইবোনাইটে অবস্থিত একটি তড়িৎ দ্বিমেরুর দুটি বিপরীত আধানের প্রত্যেকটির মান 3.2μC এবং এদের মধ্যবর্তী দূরত্ব 4cm। তড়িৎ দ্বিমেরুর অক্ষের উপর এর মধ্যবিন্দু থেকে 5cm দূরে তড়িৎ প্রাবল্যের মান (ইবোনাইট=2.8)