পরাবৃত্ত এর বিভিন্ন উপাদানসমূহ নির্ণয়
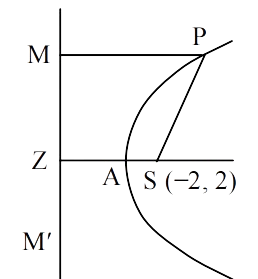
চিত্রটি একটি কনিক নির্দেশ করে যার নিয়ামক রেখা
Ai এর মাধ্যমে
১০ লক্ষ+ প্রশ্ন ডাটাবেজ
প্র্যাকটিস এর মাধ্যমে নিজেকে তৈরি করে ফেলো
উত্তর দিবে তোমার বই থেকে ও তোমার মত করে।
সারা দেশের শিক্ষার্থীদের মধ্যে নিজের অবস্থান যাচাই