লম্ব ও সমান্তরাল বিষয়ক
দুইটি সরলরেখা বিন্দু দিয়ে যায় এবং তারা রেখার সঙ্গে কোণ উৎপন্ন করে । রেখা দুইটির সমীকরণ নির্ণয় কর এবং তাদের সমীকরণ হতে দেখাও যে, তারা পরস্পর লম্বভাবে অবস্থান করে।
ধরি, বিন্দুগামী রেখার সমীকরণ
‘ +’ নিয়ে,
‘-‘ নিয়ে
রেখা দুইটির সমীকরণ,
এবং (Ans.)
এখন, রেখা দুইটির ঢালদ্বয়ের গুণফল
রেখা দুইটি পরস্পর লম্ব ভাবে অবস্থান করে।
Ai এর মাধ্যমে
১০ লক্ষ+ প্রশ্ন ডাটাবেজ
প্র্যাকটিস এর মাধ্যমে নিজেকে তৈরি করে ফেলো
উত্তর দিবে তোমার বই থেকে ও তোমার মত করে।
সারা দেশের শিক্ষার্থীদের মধ্যে নিজের অবস্থান যাচাই
একটি সরলরেখার সমীকরণ নির্ণয় কর যা -অক্ষের সমান্তরাল এবং তার নিচে 4 একক দূরে অবস্থিত।
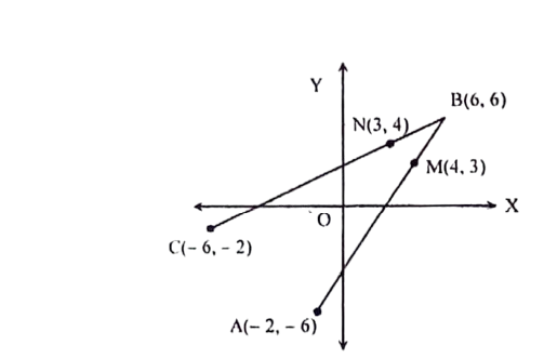
Let be a square of a side length . Let be points in the interiors of the sides respectively, such that and intersect at right angles. If then equals
বিন্দু হতে সরলরেখার উপর অঙ্কিত লম্বের পাদবিন্দুর স্থানাঙ্ক ও লম্ব দূরত্ব নির্ণয় কর।