$10^{-3} \mathrm{~cm}$

প্রস্থের 1টি চিড়ের মধ্য দিয়ে যাবার সময় ১ম অবমের জন্য 30° অপবর্তন কোণ সৃষ্টি হবে। তরঙ্গদৈর্ঘ্য কত?

অপবর্তন গ্রেটিং এর সাহায্যে-

i. তরঙ্গ দৈর্ঘ্যের সাপেক্ষে অপবর্তন কোণের পরিবর্তনের হার নির্ণয় করা যায়।

ii. তীক্ষ্ণ বর্ণালী সৃষ্টি করা যায়।

iii. নির্দিষ্ট দিকে আপতিত আলোক রশ্মিকে একত্রিত করা যায়।

নিচের কোনটি সঠিক?

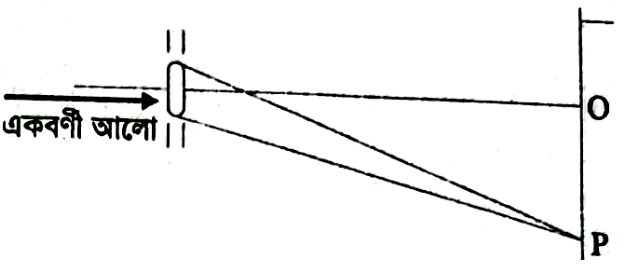
নিচের পরীক্ষণটিতে চিড়টিতে 5890Å এর আলো ফেললে 2.3 cm এ পর্দায় 20টি ঝালর দেখা যায়। যদি অন্য একটি একবর্ণী আলো ফেলা হয় তবে 2.8 cm এ পর্দার 30টি ঝালর দেখা যায়।

$10^{-3} \mathrm{~cm}$ প্রস্থের একটি চিরের ভেতর দিয়ে একটি তাড়িত চৌম্বকীয় তরঙ্গ প্রথম অবম বিন্দুর জন্য $30^{\circ}$ অপবর্তন কোণ সৃষ্টি করে। তরঙ্গটির তরঙ্গদৈর্ঘ্য কত?

একটি অপবর্তন গ্রেটিং এ প্রতি সেন্টিমিটার দৈর্ঘ্যে 3000 রেখা আছে।

তরঙ্গদৈর্ঘ্যের আলো এই গ্রেটিং এর উপর ফেলা হলো।