তড়িত বিভব
1.0m বাহু বিশিষ্ট একটি বর্গক্ষেত্রের প্রতিটি কোনায় 5×10-9c চার্জ স্থাপন করা হলো, বর্গক্ষেত্রের কেন্দ্রে বিভব নির্নয় করো.?
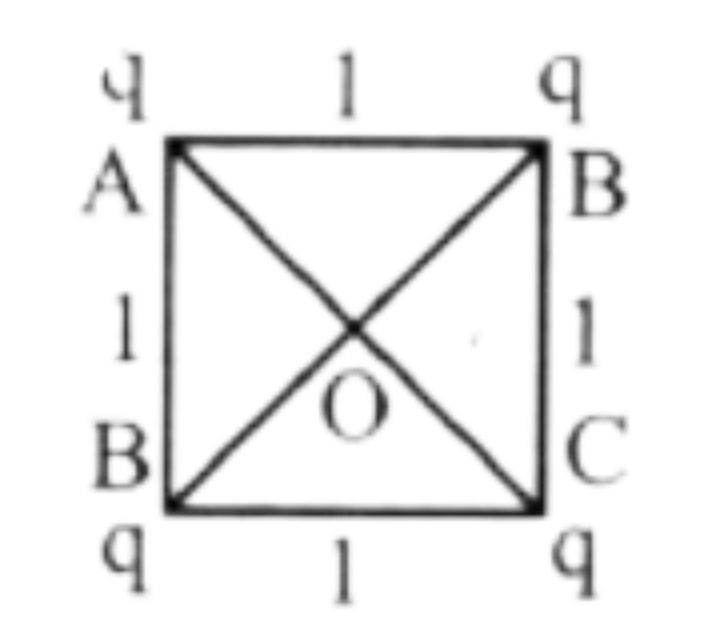
থেকে প্রতিটি কোণার দূরত্র,
বিভবের মান,
volt
Ai এর মাধ্যমে
১০ লক্ষ+ প্রশ্ন ডাটাবেজ
প্র্যাকটিস এর মাধ্যমে নিজেকে তৈরি করে ফেলো
উত্তর দিবে তোমার বই থেকে ও তোমার মত করে।
সারা দেশের শিক্ষার্থীদের মধ্যে নিজের অবস্থান যাচাই