ফ্যারাডে ও লেঞ্জের সূত্র

50 পাকবিশিষ্ট কোনো কুণ্ডলীতে 0.02 সেকেন্ডে চৌম্বক ফ্ল্যাক্স 0.03 Wb থেকে 0.025 Wb-এ পরিণত করা হলে, ঐ কুণ্ডলীতে আবিষ্ট emf কত ভোল্ট হবে?

তপন স্যার

E=−NΔΦΔt \mathcal{E}=-N \frac{\Delta \Phi}{\Delta t}

যেখানে:

- E \mathcal{E} হল আবিষ্ট তড়িৎচালক বল (ভোল্টে)

- N \quad N হল পাকের সংখ্যা (50)

- ΔΦ \Delta \Phi হল চৌম্বক ফ্লাক্সের পরিবর্তন (ওয়েবারে)

- Δt \Delta t হল সময়ের পরিবর্তন (0.02 সেকেন্ড)

প্রথমে, চৌম্বক ফ্লাক্সের পরিবর্তন (ΔΦ) (\Delta \Phi) নির্ণয় করা যাক:

ΔΦ=Φ2−Φ1=0.025 Wb−0.03 Wb=−0.005 Wb \Delta \Phi=\Phi_{2}-\Phi_{1}=0.025 \mathrm{~Wb}-0.03 \mathrm{~Wb}=-0.005 \mathrm{~Wb}

এখন, মানগুলি বসিয়ে:

E=−50×−0.0050.02E=−50×−0.0050.02=50×0.0050.02E=50×0.25=12.5 V \begin{array}{c} \mathcal{E}=-50 \times \frac{-0.005}{0.02} \\ \mathcal{E}=-50 \times \frac{-0.005}{0.02}=50 \times \frac{0.005}{0.02} \\ \mathcal{E}=50 \times 0.25=12.5 \mathrm{~V} \end{array}

অতএব, কুণ্ডলীতে আবিষ্ট তড়িৎচালক বল 12.5 ভোল্ট।

ফ্যারাডে ও লেঞ্জের সূত্র টপিকের ওপরে পরীক্ষা দাও

এখনো না বুঝতে পারলে ডাউটস এ পোস্ট করো

পোস্ট করো

Related question

আবিষ্ট তড়িচ্চালক শক্তির দিক সম্পর্কে ধারণা দেন কে? 

0.1 m × 0.05 m মানের একটি আয়তাকার কুণ্ডলীর পাক সংখ্যা 100 । এটিকে 0.1 Wbm-2 প্রাবল্যের চুম্বক ক্ষেত্রের সমকোণে রাখার পর ক্ষেত্র প্রাবল্য 0.05 sec-এ কমে 0.05 Wbm-2 হয় । তাহলে কুণ্ডলীতে আবিষ্ট তড়িচ্চালক বল কত? 

নিচের চিত্রে NS একটি দণ্ড চুম্বক, A একটি বদ্ধ কুণ্ডলী যার সাথে গ্যালভানোমিটার G যুক্ত।

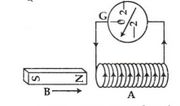
  1. চুম্বকের উত্তর মেরুকে ধীরে ধীরে কুণ্ডলীর মধ্যে প্রবেশ করালে গ্যালভানোমিটারের কাঁটা বিক্ষেপ দেখাবে
  2. চুম্বককে থামালে গ্যালভানোমিটারের কাঁটা বিক্ষিপ্ত অবস্থানে থাকবে
  3. চুম্বককে ধীরে ধীরে কুণ্ডলীর মধ্য হতে বাইরে আনলে গ্যালভানোমিটারের কাঁটা বিপরীত দিকে বিক্ষেপ দেখাবে

নিচের কোনটি সঠিক?

এক বদ্ধ কুণ্ডলীতে তড়িচ্চালক বল আবিষ্ট হয় তখনই যখন—

  1. কুণ্ডলীতে তড়িৎ প্রবাহ হ্রাস পায়
  2. কুণ্ডলীতে তড়িৎ প্রবাহ স্থির থাকে
  3. কুণ্ডলীতে তড়িৎ প্রবাহ বৃদ্ধি পায়

নিচের কোনটি সঠিক?