A body weighs $900$N on the earth. Find its weight on a planet whose density is $\dfrac{1}{3}^{st}$ the density of earth and radius is $\dfrac{1}{4}^{th}$ that of the earth.

Gravity meters measures in units of mGal where 1 Gal (or 1 galileo) is the C.G.S unit of acceleration due to gravity. A gravity meter shows a reading of +300 mGal at a place where the normal 'g' is 9.78 $m s^{-2}$. The correct 'g' at that place where the reading was taken is _____ $m s^{-2}$.

বিষুবীয় অঞ্চল থেকে মেরু অঞ্চলের দিকে অভিকর্ষীয় ত্বরণ- 

চিত্রে মসৃণ আনত তল বেয়ে গড়িয়ে পড়া বস্তুর ত্বরণ-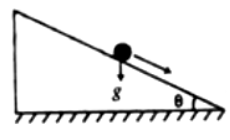 

A man weighs $'W'$ on the surface of the earth and his weight at a height $'R'$ from surface of the earth is ( R is Radius of the earth)