A player throws a ball from a height of 3.5 meters. The ball flies at a speed of 9.8 m/sec creating an angle of 30° parallel to the surface. Another player catches the ball 2.1 meters from the surface. What is the distance between those two players? Note: g = 9.8 m/sec2
IUT 11-12
v 0 x = v 0 cos ( θ ) = 9.8 cos ( 30 ∘ ) v_{0x} = v_0 \cos(\theta) = 9.8 \cos(30^\circ) v 0 x = v 0 cos ( θ ) = 9.8 cos ( 3 0 ∘ )
v 0 y = v 0 sin ( θ ) = 9.8 sin ( 30 ∘ ) v_{0y} = v_0 \sin(\theta) = 9.8 \sin(30^\circ) v 0 y = v 0 sin ( θ ) = 9.8 sin ( 3 0 ∘ )
y = y 0 + v 0 y t + 1 2 g t 2 y = y_0 + v_{0y}t + \frac{1}{2}gt^2 y = y 0 + v 0 y t + 2 1 g t 2
2.1 = 3.5 + ( 9.8 sin ( 30 ∘ ) ) t + 1 2 ( − 9.8 ) t 2 2.1 = 3.5 + (9.8 \sin(30^\circ))t + \frac{1}{2}(-9.8)t^2 2.1 = 3.5 + ( 9.8 sin ( 3 0 ∘ )) t + 2 1 ( − 9.8 ) t 2
2.1 = 3.5 + ( 9.8 × 0.5 ) t − 4.9 t 2 2.1 = 3.5 + (9.8 \times 0.5)t - 4.9t^2 2.1 = 3.5 + ( 9.8 × 0.5 ) t − 4.9 t 2
2.1 = 3.5 + 4.9 t − 4.9 t 2 2.1 = 3.5 + 4.9t - 4.9t^2 2.1 = 3.5 + 4.9 t − 4.9 t 2
4.9 t 2 − 4.9 t + ( 2.1 − 3.5 ) = 0 4.9t^2 - 4.9t + (2.1 - 3.5) = 0 4.9 t 2 − 4.9 t + ( 2.1 − 3.5 ) = 0
4.9 t 2 − 4.9 t − 1.4 = 0 4.9t^2 - 4.9t - 1.4 = 0 4.9 t 2 − 4.9 t − 1.4 = 0
t = − b ± b 2 − 4 a c 2 a t = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} t = 2 a − b ± b 2 − 4 a c a = 4.9 a = 4.9 a = 4.9 b = − 4.9 b = -4.9 b = − 4.9
c = − 1.4 c = -1.4 c = − 1.4
t = − ( − 4.9 ) ± ( − 4.9 ) 2 − 4 ( 4.9 ) ( − 1.4 ) 2 ( 4.9 ) t = \frac{-(-4.9) \pm \sqrt{(-4.9)^2 - 4(4.9)(-1.4)}}{2(4.9)} t = 2 ( 4.9 ) − ( − 4.9 ) ± ( − 4.9 ) 2 − 4 ( 4.9 ) ( − 1.4 )
t = 4.9 ± 24.01 + 27.44 9.8 t = \frac{4.9 \pm \sqrt{24.01 + 27.44}}{9.8} t = 9.8 4.9 ± 24.01 + 27.44
t = 4.9 ± 51.45 9.8 t = \frac{4.9 \pm \sqrt{51.45}}{9.8} t = 9.8 4.9 ± 51.45
t = 4.9 ± 7.1728 9.8 t = \frac{4.9 \pm 7.1728}{9.8} t = 9.8 4.9 ± 7.1728
t = 4.9 + 7.1728 9.8 = 12.0728 9.8 ≈ 1.2319 s t = \frac{4.9 + 7.1728}{9.8} = \frac{12.0728}{9.8} \approx 1.2319 \text{ s} t = 9.8 4.9 + 7.1728 = 9.8 12.0728 ≈ 1.2319 s
x = v 0 x t x = v_{0x}t x = v 0 x t
x = ( 9.8 cos ( 30 ∘ ) ) × 1.2319 x = (9.8 \cos(30^\circ)) \times 1.2319 x = ( 9.8 cos ( 3 0 ∘ )) × 1.2319
x = ( 9.8 × 3 2 ) × 1.2319 x = \left(9.8 \times \frac{\sqrt{3}}{2}\right) \times 1.2319 x = ( 9.8 × 2 3 ) × 1.2319
x ≈ ( 9.8 × 0.866 ) × 1.2319 x \approx (9.8 \times 0.866) \times 1.2319 x ≈ ( 9.8 × 0.866 ) × 1.2319
x ≈ 8.487 × 1.2319 ≈ 10.45 m x \approx 8.487 \times 1.2319 \approx 10.45 \text{ m} x ≈ 8.487 × 1.2319 ≈ 10.45 m
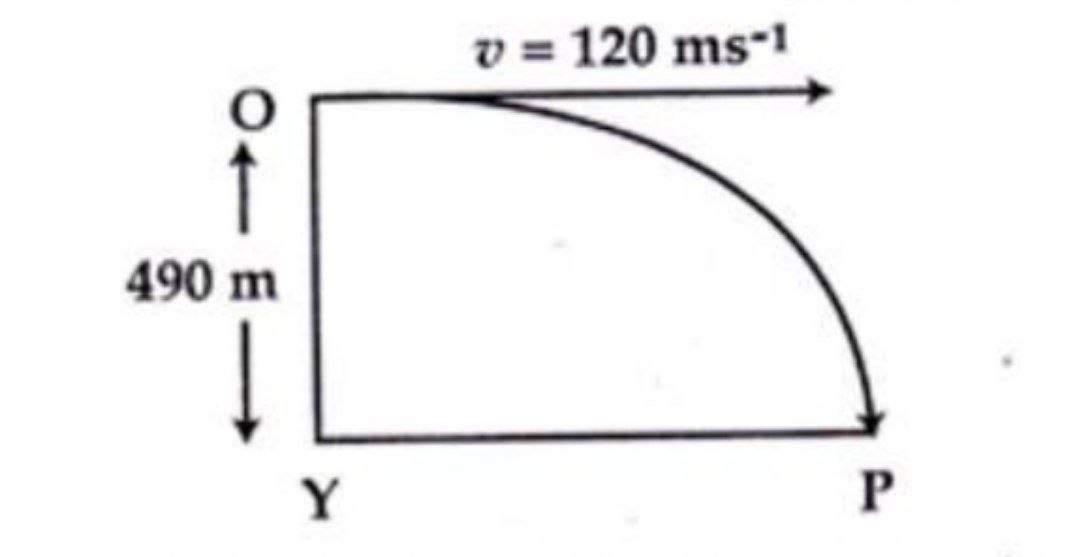
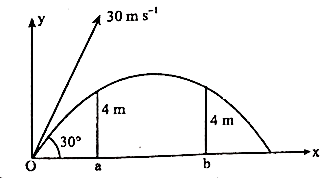
 প্রক্ষিপ্ত বিন্দু ও বিচরণ পথের শেষ প্রান্ত বিন্দুর মধ্যবর্তী অনুভূমিক দূরত্বকে অনুভূমিক পাল্লা বলে। অনুভূমিক পাল্লা
প্রক্ষিপ্ত বিন্দু ও বিচরণ পথের শেষ প্রান্ত বিন্দুর মধ্যবর্তী অনুভূমিক দূরত্বকে অনুভূমিক পাল্লা বলে। অনুভূমিক পাল্লা