ক্রস গুণন
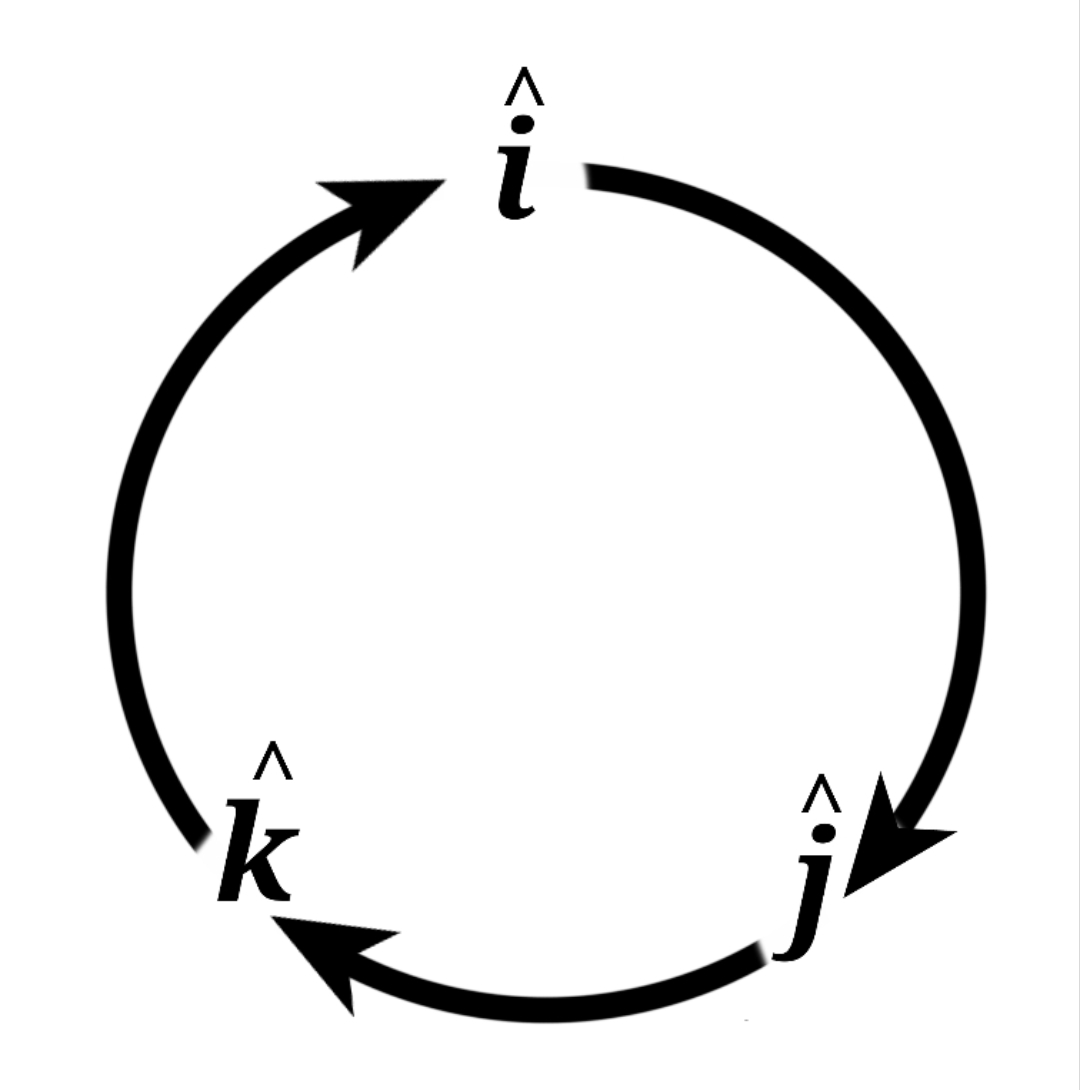 Clockwise গুণ করলে ধনাত্মক ও anti clockwise গুণ করলে ঋণাত্মক মান পাওয়া যাবে।
Clockwise গুণ করলে ধনাত্মক ও anti clockwise গুণ করলে ঋণাত্মক মান পাওয়া যাবে।
Ai এর মাধ্যমে
১০ লক্ষ+ প্রশ্ন ডাটাবেজ
প্র্যাকটিস এর মাধ্যমে নিজেকে তৈরি করে ফেলো
উত্তর দিবে তোমার বই থেকে ও তোমার মত করে।
সারা দেশের শিক্ষার্থীদের মধ্যে নিজের অবস্থান যাচাই