Loading ...
তড়িতশক্তি ও ক্ষমতা
1. 
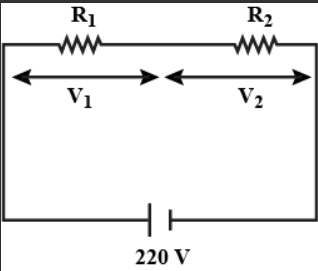
In the above question, Find individual power consumed.
Given and
Ai এর মাধ্যমে
১০ লক্ষ+ প্রশ্ন ডাটাবেজ
প্র্যাকটিস এর মাধ্যমে নিজেকে তৈরি করে ফেলো
উত্তর দিবে তোমার বই থেকে ও তোমার মত করে।
সারা দেশের শিক্ষার্থীদের মধ্যে নিজের অবস্থান যাচাই
ও
এর ২টি বাল্ব 1টি 220V উৎসের সাথে শ্রেণিতে যুক্ত আছে।
When the balance point is obtained in the potentiometer, a current is drawn from
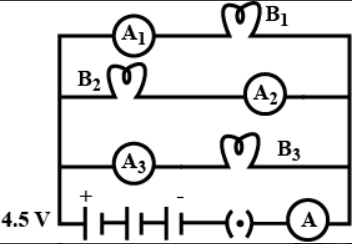
and are three identical bulbs connected as shown in Figure 12.8. When all the three bulbs glow, a current of 3A is recorded by the ammeter A.
How much power is dissipated in the circuit when all the three bulbs glow together?
The resistance of the filament of an electric bulb changes with temperature. If an electric bulb rated and is connected to source, then the power would be :
