দুইটি বলের লব্ধির মান ও কোণ
P মানের দুইটি বলের লব্ধি
এদের যেকোন একটির সাথে লব্ধির নতি কোনটি?
লব্ধির সাথে একটি বলের মধ্যবর্তী কোণ ϕϕ হলে, আমরা নিম্নলিখিত সূত্র ব্যবহার করি:
হলেঃ
ϕ=22.5∘
Ai এর মাধ্যমে
১০ লক্ষ+ প্রশ্ন ডাটাবেজ
প্র্যাকটিস এর মাধ্যমে নিজেকে তৈরি করে ফেলো
উত্তর দিবে তোমার বই থেকে ও তোমার মত করে।
সারা দেশের শিক্ষার্থীদের মধ্যে নিজের অবস্থান যাচাই
কোন বিন্দুতে 3N এবং 4N দুইটি বল পরস্পর 60°
কোণে কার্যরত থাকলে-
বলদ্বয়ের লব্ধির মান নিউটন
প্রথম বলের দিক বরাবর দ্বিতীয় বলের আনুভূমিক উপাংশ = 2
বলদ্বয়ের লব্ধির ক্রিয়ারেখা প্রথম বলের ক্রিয়া রেখার সাথে 34.715° কোণ উৎপন্ন করে
নিচের কোনটি সঠিক?
দৃশ্যকল্প-১ : একটি বিন্দুতে মানের দুইটি বল কোণে ক্রিয়ারত হলে লব্ধি এবং কোণে ক্রিয়ারত হলে লব্ধি .
দৃশ্যকল্প-২ : P ও মানের দুইটি বিপরীতমুখী সমান্তরাল বল A ও B বিন্দুতে ক্রিয়ারত।
3P ও 4P মানের দুইটি বল একটি কণার উপর α কোণে ক্রিয়া করে। তাদের লব্ধি হলে α এর মান কত?
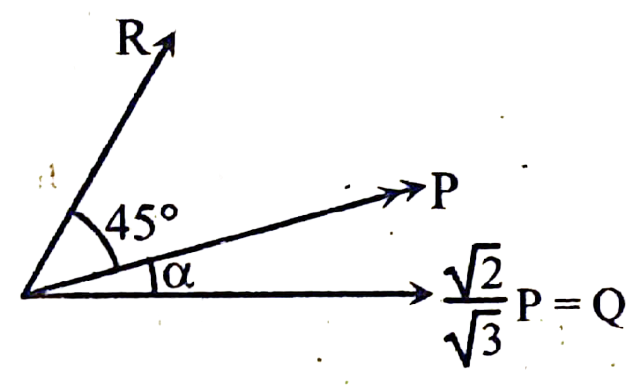
R ও Q, P এর দুটি অংশক হলে, α এর মান কত?