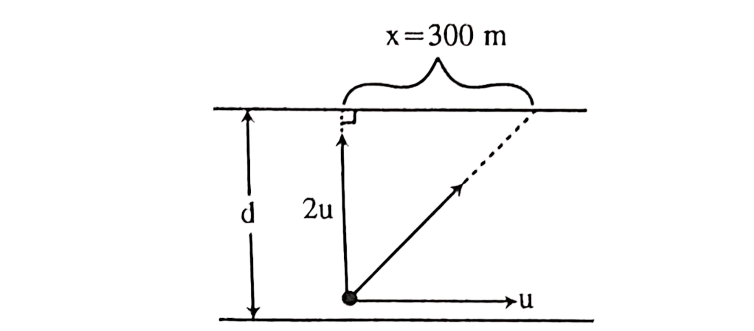
Suppose, your swimming velocity is twice of current in a river. You wish to cross the river perpendicularly having the current. But you reached 300 m far from the opposite of your starting point. Then width of the r

iver is-

[উভয় চিত্রে $v=$ নৌকার বেগ $=6 \mathrm{~ms}^{-1} ; R=$ লব্ধি বেগ]

1 km প্রস্থের একটি নদী পার হওয়ার জন্য দুইজন সাতারু, সাঁতার প্রতিযোগিতায় অংশগ্রহণ করে। প্রথম সাঁতারু 6 kmh^-1 বেগে স্রোতের প্রতিকূলের সাথে 60°কোণে এবং দ্বিতীয় সাঁতারু 6 kmh^-1 বেগে আড়াআড়িভাবে সাঁতার কাটা শুরু করে। নদীতে স্রোতের বেগ 3kmh^-1।

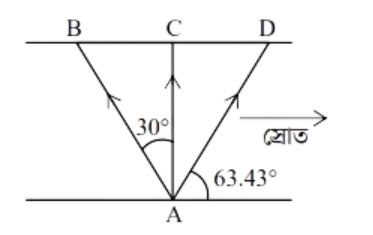
চিত্রানুযায়ী একটি নদী 31 km প্রশস্ত। দুটি ইঞ্জিন চালিত বোট আড়াআড়ি পার হওয়ার জন্য A হতে অভিন্ন বেগে যাত্রা শুরু করল, যাদের একটি AB বরাবর অপরটি AC বরাবর।

প্রথমটি আড়াআড়ি পার হয়ে C বিন্দুতে পৌছাঁলেও দ্বিতীয়টি D বিন্দুতে পৌঁছায়। [স্রোতের বেগ $9~kmh^{-1}$]

$10 \mathrm{~km}$ প্রস্থবিশিষ্ট একটি নদীতে ল্রোতের বেগ $5 \mathrm{kmh}^{-1}$ । প্রথম মাঝি $10 \mathrm{kmh}^{-1}$. বেগে ম্রোতের সাথে $\alpha$ কোণে এবং ২য় মাঝি $10 \mathrm{kmh}^{-1}$ বেগে স্রোতের সাথে লম্বভাবে নদী পার হতে যাত্রা করল।কে আগে পৌঁছাবে?