কোণ ও দিক নির্ণয়

The angle of incidence on the plane mirror is 30. The angle between the incident ray and the reflected ray is:

হানি নাটস

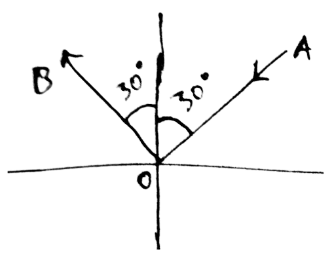
Incident ray =AO‾ =\overline{A{O}}

Reflected ray =OB‾ =\overline{O B}

∴ \therefore Angle between

 Incident and reflected ray =30∘+30∘=60∘ \begin{aligned} \text { Incident and reflected ray } & =30^{\circ}+30^{\circ} & =60^{\circ}\end{aligned}

কোণ ও দিক নির্ণয় টপিকের ওপরে পরীক্ষা দাও

এখনো না বুঝতে পারলে ডাউটস এ পোস্ট করো

পোস্ট করো

Related question

 A⃗=2i^+2j^−k^ \vec{A} = 2 \hat{i} + 2 \hat{j} - \hat{k} এবং  B⃗=6i^−3j^+2k^ \vec{B} = 6 \hat{i} - 3 \hat{j} + 2 \hat{k}  হলে A⃗ \vec{A} ও B⃗ \vec{B} এর মধ্যবর্তী কোণের মান কত?

চিত্রে দুটি বিন্দু P P ও Q Q এর স্থানাঙ্ক দেওয়া আছে। OP→ \overrightarrow{O P} ও OQ→ \overrightarrow{O Q} যথাক্রমে বিন্দুদ্বয়ের অবস্থান ভেক্টর নির্দেশ করছে।

যদি  P⃗=2i^+4j^−5k^ \vec{P} = 2 \hat{i} + 4 \hat{j} - 5 \hat{k} এবং  Q⃗=i^+2j^+3k^ \vec{Q} = \hat{i} + 2 \hat{j} + 3 \hat{k} হয় তবে এদের মধ্যবর্তী কোণ-  

A⃗=4i^+5k^ \vec{A}=4 \hat{i}+5 \hat{k} ভেক্টরটি z অক্ষের সাথে কত ডিগ্রী কোন উৎপণ্ন করে?