1. একটি এয়ারকন্ডিশনিং ইউনিট ছাদের ওপর দড়ি দিয়ে বেঁধে রাখা আছে| ইউনিটির ওজনের উল্লম্ব উপাংশ সর্বোচ্চ 425N হতে পারবে অন্যথায় বস্তুটি ছাদের টিন মুছড়ে নিচে পড়ে যাবে| কোনো বস্তুকে হেলানো তলে রাখলে বস্তুটির ওজন হেলানো দলের উল্লম্ব ও আনুভূমিক দুটি উপাংশে বিভক্ত হয়|
2. 
4. (ক) দুটি ভেক্টর এর ক্রস গুণফল  শূন্য হওয়ার শর্ত কি ?
   (খ) যদি A→ এবং B→ এর মান শূন্য না হয় তাহলে কি একই সাথে a→×b→ শূন্য হতে পারবে ? 
   (গ) এয়ারকন্ডিশনিং ইউনিটের সর্বোচ্চ ওজন কত হতে পারবে ? 
   (ঘ) দড়ি যদি ছিড়ে যায় তাহলে এয়ার কন্ডিশনিং ইউনিটটি ছাদের কার্নিশে এসে থামবে এক্ষেত্রে বস্তুটির ওজন বল কি পরিমান কাজ করবে ? 

সমাধান (ক)
দুটি ভেক্টরের ক্রস গুণফল শূন্য হবে যদি এই দুটি ভেক্টর পরস্পরের সাথে সমান্তরাল হোন
সমাধান (খ)

হ্যাঁ, এটি সম্ভব। ভেক্টর গুণফল শূন্য হতে পারে এমনকি যদি ভেক্টরগুলির দৈর্ঘ্য শূন্য না হওয়াও। ক্রস গুণফল A × B হল ভেক্টর A এবং B এর দৈর্ঘ্য গুণিত তাদের মধ্যবর্তী কোণের সাইন। অর্থাৎ, এটি |A||B|sin(θ) এর সমান, যেখানে |A| এবং |B| হল ভেক্টর A এবং B এর দৈর্ঘ্য, এবং θ হল এদের মধ্যে কোণ।

যদি এই দুটি ভেক্টর পরস্পরের সাথে সমান্তরাল হোন (অর্থাৎ, এদের মধ্যে কোণ 0 ডিগ্রি অথবা 180 ডিগ্রি), তাহলে sin(θ) এর মান 0 হবে এবং তাই A × B = 0 হবে, এমনকি যদি |A| এবং |B| শূন্য না হওয়াও। এই ক্ষেত্রে, আমরা বলি যে ভেক্টরগুলি "সমান্তরাল" বা একই দিকে নেই।

(গ) সমাধান

 
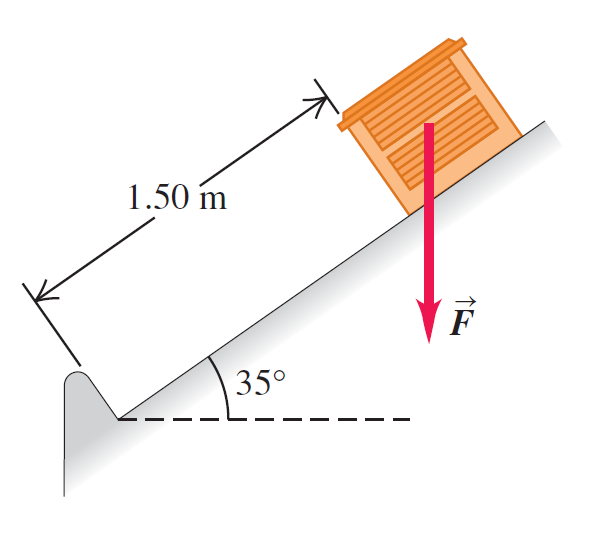
Fcosθ=425F=425cos35

(ঘ) সমাধান 
W=mgsinθ=425cos35sin35=425tan35