অন্তরীকরণ এর অন্যান্য
Find 'c' of the mean value theorem, if
We have and
Now
Putting all these value in lagrange's mean value theorem
We get
Hence lies in the open interval
Therefore it is the required value
Ai এর মাধ্যমে
১০ লক্ষ+ প্রশ্ন ডাটাবেজ
প্র্যাকটিস এর মাধ্যমে নিজেকে তৈরি করে ফেলো
উত্তর দিবে তোমার বই থেকে ও তোমার মত করে।
সারা দেশের শিক্ষার্থীদের মধ্যে নিজের অবস্থান যাচাই
বক্র রেখার উপর একটি বিন্দু নির্ণয় কর যা বিন্দুর সর্বোচ্চ নিকটবর্তী।
M ক্ষেত্রের উর্বরতা N ক্ষেত্রের উর্বরতার দ্বিগুণ। M ক্ষেত্রের একটি আয়তাকার ভূমি, N ক্ষেত্রে সমান
উৎপাদনশীল একটি বর্গাকার ভূমির সংগে বিনিময় করতে হলে বর্গাকার ভূমির দৈর্ঘ্য কত m হতে হবে?
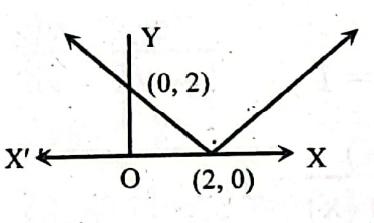
লেখচিত্রটির অন্তরজ নিচের কোনটি?
একটি আয়তক্ষেত্রের দৈর্ঘ্য প্রস্থের দ্বিগুণ, এর পরিসীমা সেকেন্ডে 9cm হারে এবং ক্ষেত্রফল সেকেন্ডে 16cm2 হারে বৃদ্ধি পেলে আয়তক্ষেত্রের দৈর্ঘ্য ও প্রস্থ কত হবে?