উপবৃত্ত এর সমীকরণ নির্ণয়
The y-axis is the directrix of the ellipse with eccentricity e=1/2 and the corresponding focus is at (3, 0), equation to its auxilary circle is
Given that y-axis is the directrix.
⇒x=0
We know that directrix is x=h−ae
So, ⇒h−ae=0
⇒h=ae
⇒h=a1/2
⇒h=2a
We know that focus =(h−ae,k)
⇒(h−ae,k)=(3,0)
⇒h−ae=3
⇒2a−(a/2)=3
⇒3a/2=3
⇒a=2
⇒a2=4
We know that b^2=a^2(1−e^2)
⇒h=2a=4;k=0
⇒b^2=4(1−1/4)
⇒
b^2=3
So, equation of ellipse⇒(x−4)^2/4+y²/3=1
Hence, equation of auxiliary circle is ⇒(x−h)^2+(y−k)^2=a^2
⇒(x−4)^2+y^2=4
⇒x^2+y^2−8x+16=4
⇒x^2+y^2−8x+12=0
Ai এর মাধ্যমে
১০ লক্ষ+ প্রশ্ন ডাটাবেজ
প্র্যাকটিস এর মাধ্যমে নিজেকে তৈরি করে ফেলো
উত্তর দিবে তোমার বই থেকে ও তোমার মত করে।
সারা দেশের শিক্ষার্থীদের মধ্যে নিজের অবস্থান যাচাই
The eccentricity of an ellipse, with its centre at the origin, is. If one of the directrices is x = 4, then the equation of the ellipse is
উদ্দীপক -১: একটি কণিকের উপকেন্দ্র (0, ±4) এবং উৎকেন্দ্রিকতা (4 / 5)
উদ্দীপক-২: f(x, y) = 4x2 + 9y2 – 8x – 36y + 4 = 0
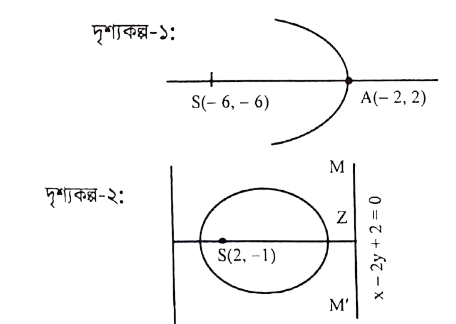
দৃশ্যকল্প-১: তিনটি বিন্দু এবং
দৃশ্যকল্প-২: একটি সরলরেখার সমীকরণ