ত্রিভুজের ক্ষেত্রফল
If the area of a triangle formed by the points (k, 2k) (-2, 6) and (3, 1) is 20 square units. Find the value of k.
Area of a triangle with vertices , and is
Hence, area of the triangle with given vertices
Ai এর মাধ্যমে
১০ লক্ষ+ প্রশ্ন ডাটাবেজ
প্র্যাকটিস এর মাধ্যমে নিজেকে তৈরি করে ফেলো
উত্তর দিবে তোমার বই থেকে ও তোমার মত করে।
সারা দেশের শিক্ষার্থীদের মধ্যে নিজের অবস্থান যাচাই
Find the value of if the points and are collinear.
The area of the triangle whose co-ordinates are and is unit. The sum of possible values of is
নিচের তথ্যের আলোকে প্রশ্নটির উত্তর দাওঃ
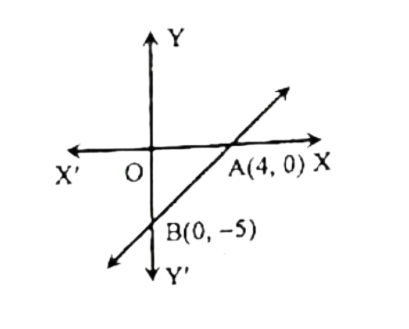 এর ক্ষেত্রফল কত বর্গ একক?
এর ক্ষেত্রফল কত বর্গ একক?
Let and be the vertices of a right- angled triangle with as its hypotenuse.
If the area of the triangle is 1, then the set of values which can take is given by-