ত্রিভুজের ক্ষেত্রফল
If area of a triangle is square units with vertices and then is :
Area of triangle sq.units
Ou Taking +ve sign,
On taking - ve sign,
Ai এর মাধ্যমে
১০ লক্ষ+ প্রশ্ন ডাটাবেজ
প্র্যাকটিস এর মাধ্যমে নিজেকে তৈরি করে ফেলো
উত্তর দিবে তোমার বই থেকে ও তোমার মত করে।
সারা দেশের শিক্ষার্থীদের মধ্যে নিজের অবস্থান যাচাই
Find the value of if the points and are collinear.
The area of the triangle whose co-ordinates are and is unit. The sum of possible values of is
If the area of a triangle formed by the points (k, 2k) (-2, 6) and (3, 1) is 20 square units. Find the value of k.
নিচের তথ্যের আলোকে প্রশ্নটির উত্তর দাওঃ
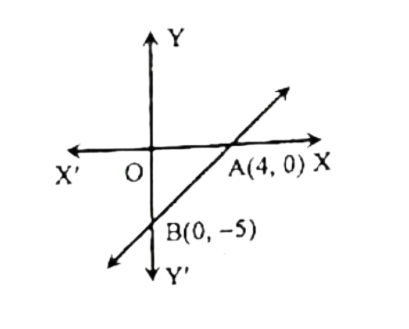 এর ক্ষেত্রফল কত বর্গ একক?
এর ক্ষেত্রফল কত বর্গ একক?